Statistics can be a useful tool when performing Data Science (DS). Statistics, in its broadest sense, is the application of mathematics to the technical analysis of data. A simple visualisation, such as a bar chart, may provide some high-level information, but statistics allow us to operate on the data in a much more information-driven and targeted manner. Instead of guessing, the math involved allows us to form concrete conclusions about our data.
We can use statistics to gain deeper and finer-grained insights into how our data is structured and, based on that structure, how we can best apply other data science techniques to obtain even more information. Today, we’ll look at 5 fundamental statistics concepts that data scientists must understand and how they can be applied most effectively!
Statistical Characteristics
Statistical features are most likely the most commonly used statistics concept in data science. It is frequently the first stats technique used when exploring a dataset and includes terms such as bias, variance, mean, median, percentiles, and many others. It’s all fairly simple to understand and code! For an illustration, see the graphic below.
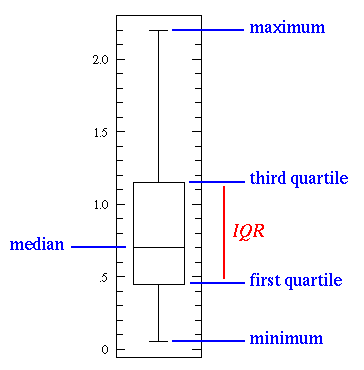
A Simple Box Plot
The line in the middle represents the data’s median value. The median is preferred over the mean because it is more resistant to outlier values. The first quartile is equivalent to the 25th percentile; that is, 25% of the data points fall below that value. The third quartile is the 75th percentile, which means that 75% of the data points fall below that value. The min and max values represent the upper and lower limits of our data range, respectively.
A box plot is an excellent example of what we can do with basic statistical features:
- Because there are many values in a small range, a short box plot implies that many of your data points are similar.
- When the box plot is tall, it indicates that many of your data points are quite different, as the values span a wide range.
- If the median value is near the bottom, we know that the majority of the data has lower values. If the median value is near the top, we know that the majority of the data has higher values. If the median line is not in the centre of the box, it indicates that the data is skewed.
- Are the whiskers particularly long? That means your data has a high standard deviation and variance, indicating that the values are dispersed and highly variable. If one side of the box has long whiskers but not the other, your data may be highly varying only in one direction.
All based on a few simple statistical features that are simple to calculate! Use these whenever you need a quick but informative look at your data.
Distributions of Probability
Probability is defined as the percentage chance that an event will occur. In data science, this is commonly quantified on a scale of 0 to 1, with 0 indicating that we are certain this will not occur and 1 indicating that we are certain it will occur. A probability distribution is then a function that represents the probabilities of all possible experiment values. For an illustration, see the graphic below.
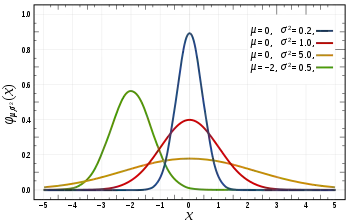
The most fundamental of the three shown here is a Uniform Distribution. It has a single value that only occurs within a certain range, and anything outside of that range is simply 0. It is strictly a “on or off” distribution. It can also be viewed as an indication of a categorical variable with two options: 0 or the value. Even if your categorical variable has multiple values other than 0, we can still visualise it as a piecewise function of multiple uniform distributions.
- A Normal Distribution, also known as a Gaussian Distribution, is defined specifically by its mean and standard deviation. The mean value spatially shifts the distribution, while the standard deviation controls the spread. The standard deviation is the same in all directions, which distinguishes it from other distributions (for example, poisson). With a Gaussian distribution, we can determine the average value of our dataset as well as its spread, or whether it is highly concentrated around a few values.
- A Poisson Distribution is similar to a Normal Distribution, but with the addition of skewness. A poisson distribution, like the Normal, will have a relatively uniform spread in all directions if the skewness is low. However, when the skewness value is large, the spread of our data will be different in each direction; in one direction, it will be very spread, while in the other, it will be highly concentrated.
- There are many more distributions into which you can delve, but those three provide us with a lot of value. With a Uniform Distribution, we can quickly see and interpret our categorical variables. When we see a Gaussian Distribution, we know that there are many algorithms that will perform well by default with Gaussian, and we should use those. And with Poisson, we’ll see that we need to be extra cautious and select an algorithm that is resistant to variations in the spatial spread.
Reduced Dimensionality
Dimensionality Reduction is a simple concept to grasp. We have a dataset and want to reduce the number of dimensions in it. This is the number of feature variables in data science. For an illustration, see the graphic below.
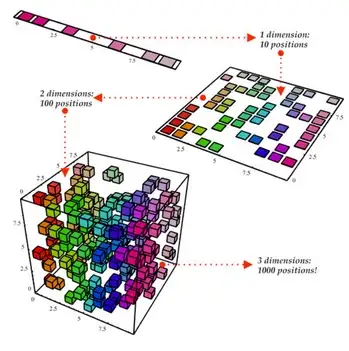
Reduced Dimensionality
Our dataset is represented by a cube, which has three dimensions and a total of 1000 points. With today’s computing power, 1000 points are simple to process, but on a larger scale, we’d run into issues. Looking at our data from a 2-Dimensional perspective, such as one side of the cube, we can see that it’s quite simple to divide all of the colours from that angle. We would then use dimensionality reduction to project the 3D data onto a 2D plane. This effectively reduces the number of points we need to compute on to 100, saving us a significant amount of time!
Feature pruning is another method for reducing dimensionality. With feature pruning, we essentially want to remove any features that we believe will be irrelevant to our analysis. For example, after examining a dataset, we may discover that seven of the ten features have a high correlation with the output, while the remaining three have a very low correlation. Then those three low correlation features are probably not worth computing, and we may be able to remove them from our analysis without affecting the output.
PCA, the most commonly used statistics technique for dimensionality reduction, essentially creates vector representations of features that show how important they are to the output, i.e. their correlation. PCA can be used to perform both of the dimensionality reduction techniques discussed previously. More information can be found in this tutorial.
Under and Over Sampling
Over and under sampling are classification problem techniques. Our classification dataset may occasionally be too heavily skewed to one side. We have 2000 examples for class 1, but only 200 for class 2. That will throw off a lot of the Machine Learning techniques we try to use to model the data and predict outcomes! Our Over and Under Sampling can help. For an illustration, see the graphic below.
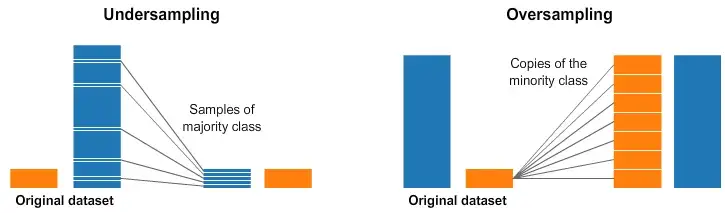
Over and Under Sampling
Our blue class has far more samples than the orange class on both the left and right sides of the image above. In this case, we have two pre-processing options to help train our Machine Learning models.
Undersampling means taking only a subset of the data from the majority class and using only as many examples as the minority class has. This selection should be made in order to preserve the class’s probability distribution. That was simple! We simply evened out our dataset by taking fewer samples!
Oversampling means making duplicates of our minority class in order to have the same number of examples as the majority class. The copies will be made in such a way that the minority class’s distribution is preserved. We simply evened out our dataset without adding any new data!
Statistics Using Bayesian Methods
To fully comprehend why we use Bayesian Statistics, we must first understand where Frequency Statistics fails. When most people hear the word “probability,” they immediately think of frequency statistics. It entails using math to calculate the likelihood of an event occurring, with the only data we compute on being prior data.

Consider the following example. Assume I gave you a die and asked you what your chances were of rolling a 6. Most people would simply say it’s 1 in 6. Indeed, if we did a frequency analysis, we would look at some data where someone rolled a die 10,000 times and compute the frequency of each number rolled; it would come out to roughly one in six!
But what if someone told you that the die you were given was programmed to always land on 6? Because frequency analysis only considers prior data, the evidence that you were given about the die being loaded is ignored.
This evidence is taken into account by Bayesian statistics. We can see this in action by considering Baye’s theorem:
Theorem of Bayes
In our equation, the probability P(H) represents our frequency analysis; given our prior data, what is the probability of our event occurring? The P(E|H) in our equation is known as the likelihood, and it represents the likelihood that our evidence is correct given the information from our frequency analysis. For example, if you wanted to roll the die 10,000 times and got all 6 on the first 1000 rolls, you’d be pretty confident that the die is loaded! The P(E) represents the likelihood that the actual evidence is correct. Can you believe me when I say the die is loaded, or do you think I’m playing a trick on you?
If our frequency analysis is very good, it will have some weight in indicating that our guess of 6 is correct. At the same time, we consider our evidence of the loaded die, whether it is true or false based on both its own prior and the frequency analysis. As you can see from the layout of the equation, Bayesian statistics considers everything. Use it whenever you suspect that your previous data will not accurately represent your future data and results.


